Stable and nonstable momentum (optional material)
Espenshade and colleagues (2011) recently decomposed momentum into two constituent and multiplicative parts called "stable" and "nonstable" momentum, which shed more light on the sources of future growth. Nonstable momentum quantifies the deviation between a population's current age distribution and the stable age distribution implied by current fertility and mortality conditions. Stable momentum, on the other hand, quantifies the change between the stable age distribution and the stationary age distribution produced by replacement fertility.
Nonstable momentum thus reflects a nation's recent population history. Countries that experienced a recent and sharp fertility decline with clear traces in the population age structure will have relatively large values for nonstable momentum. In a stable population where fertility has been constant for a long time, nonstable momentum is negligible. The value for stable momentum is entirely dependent on a population's current fertility and mortality levels: a population with a high NRR will have a large value for stable momentum and vice versa.
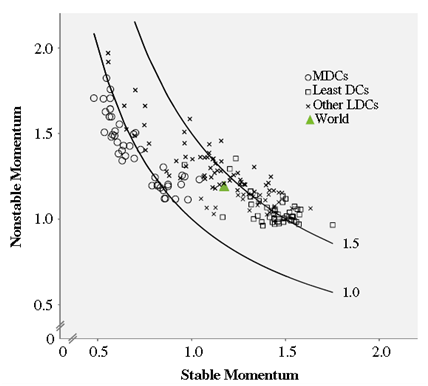
Figure 5. Plot of stable and nonstable momentum for individual countries by level of development, 2005 (N-176 countries). MDCs: more developed countries; LDCs: less-developed countries. The two isoquants represent total momentum of 1 and 1.5.
Source: Espenshade et al. 2011
The figure above plots stable against nonstable momentum for 176 countries in 2005. This plot that total momentum is larger in Least Developed Countries and lowest in the Most Developed Countries. Interestingly, the total momentum in Least Developed Countries is almost entirely produced by stable momentum. The reason is that many of these countries have not experienced any sharp declines in fertility rates in the recent past, and their population age structures are close to stable.
In the Most Developed Countries, total momentum is close to 1, but stable momentum is often below unity, indicating that their current fertility and mortality regimes would eventually lead to population shrinkage. Values of nonstable momentum greater than unity will largely offset the population decline provided that fertility rates were immediately raised to replacement level.